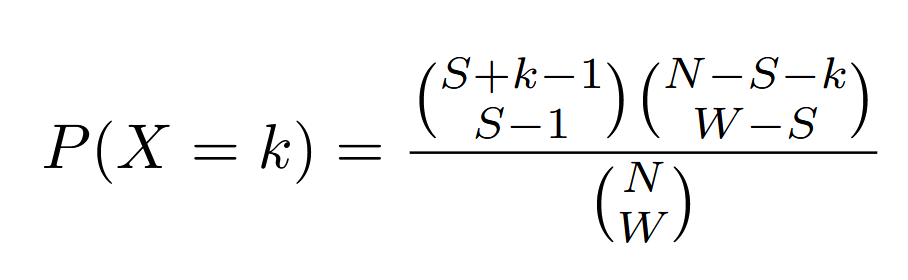
What is the Negative Hypergeometric Distribution?

Background

The Negative Hypergeometric Distribution is the most confusing distribution you'll likely ever encounter in a probability class. Even the name is intimidating. It took me much, much, longer to understand it than anything else we covered, and I did not see an explanation I found straightforward and satisfactory anywhere on the internet or in my textbook. I hope to tell a coherent story about this distribution that explains where it comes from and why it has, perhaps, the ugliest Probability Mass Function you are likely to encounter.

This isn't meant to be an especially rigorous or proof-based article, just an easy to understnad introduction

Also, before we continue, some vocabulary to know:

• Probability Mass Function: A probability distribution for a discrete random variable, telling you what the odds are of an event. For example, you may want to know the chance a coin flipped three times will result in three heads, or P(X = 3). We use a probability mass function when dealing with things that come in some quantized amount, like balls or coin tosses or dice rolls.
• Probability Density Function: This isn't strictly relevant for this topic, but if we were to deal with a Random Variable that can come in arbitrarily small quantities, like temperature or volume, then it wouldn't make much sense to assign probabilities to a specific value. Instead, we would use a Probability Density Function to describe P(X < k)

When to use the Negative Hypergeometric Distribution?

The Negative Hypergeometric Distribution is used when you want to know the odds of it taking k trials to achieve some fixed number of successes. Remember that a distribution has parameters and takes a variable. The variable taken by the Negative Hypergeometric Distribution is the number of trials beyond the number of successes, with the number of successes being baked into the trial itself. This is in contrast to the non-negative distributions, where you specify a number of trials in the distribution itself and estimate the number of successes.

For example, assume you're looking through a bowl of Starburst until you can find five of red, your favorite flavor. Whenever you remove one from the bowl to look at it, you place it to the side. . You couldn't use the Negative Binomial distribution, because you're not placing the starburst back in the bowl. The regular non-negative Hypergeometric distribution also wouldn't work, given that you don't know how many candies you plan to draw. We'll need something different to attempt a problem like this.

This all will make more sense once you see the distribution itself, don't worry.

The Distribution Itself

Take the distribution \[NegHyperGeo \sim (W, N, S) \]

Let's use the analogy of picking balls out of an urn. In this distribution, we have W White balls out of N Number of balls total. Of these, we are hoping to get S Successes. Assume we want to know the odds that, if we do X+S trials, we will get S successes. This is the Negative Hypergeometric distribution, featured below.

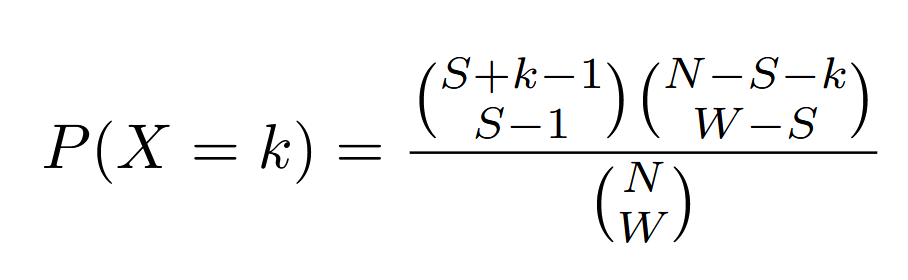
What's confusing is that k is NOT the number of trials; it's the number of trials after you have done S trials. So, P(X = 0) is not the probability you get S balls in no trials, but the probability you get S balls in S trials, with the Sth trial being a success. P(X = 3) is the odds that, you do S + 3-1 trials, get S - 1 successes, and then on the S+3rd trial you get your Sth success.

Now that we have a definition of k, it should be clear that the PMF only applies for \( k = 0, 1, 2, ... (N-S) \), and in all other cases P(X = k) is 0. To get S successes, you need at least S trials, but if k>N-S, then you would run out of balls.

Do also note that this is a Discrete distribution, so it makes no sense to talk about non-integer values of k.

The Distribution Broken Down

In most probability distributions, you can kind of look at the PMF and see what each component is doing. The Negative Hypergeometric Distribution's PMF is a bit more complicated, but nevertheless can be broken down and understood.

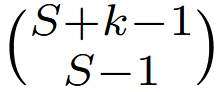
This is, in effect, saying that we take the number of successes we want, add k, the additional number of balls we are removing from our figurative urn, and then subtract 1. S + k is fairly self-explanitory, as we are trying to see the number of ways to choose that many successes. The -1 comes in, a bit more confusingly, as we are only looking at selections before S+k, rather than at S+k itself. We want to know that, if the S+kth draw is a success, then how many ways can we arrange the S-1 successes before it. That is the story of the first choice function in the PMF.

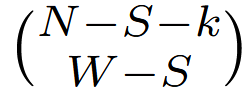
What this tells us is that, out of N-S-k (Total Number - Successes Drawn- Additional draws), how many ways can you arrange the remaining white balls. N-S-k, tells us how many balls total are remaining in the urn after our random variable k number of draws. W-S tells us how many white balls are remaining after our S+k draws.

With this, we have the entire numerator complete. This is the total number of permutations possible with S successes in S + k draws. The only thing remaining is to divide it by the total number of permutations possible

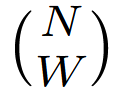
Putting it all together, this gets us to.

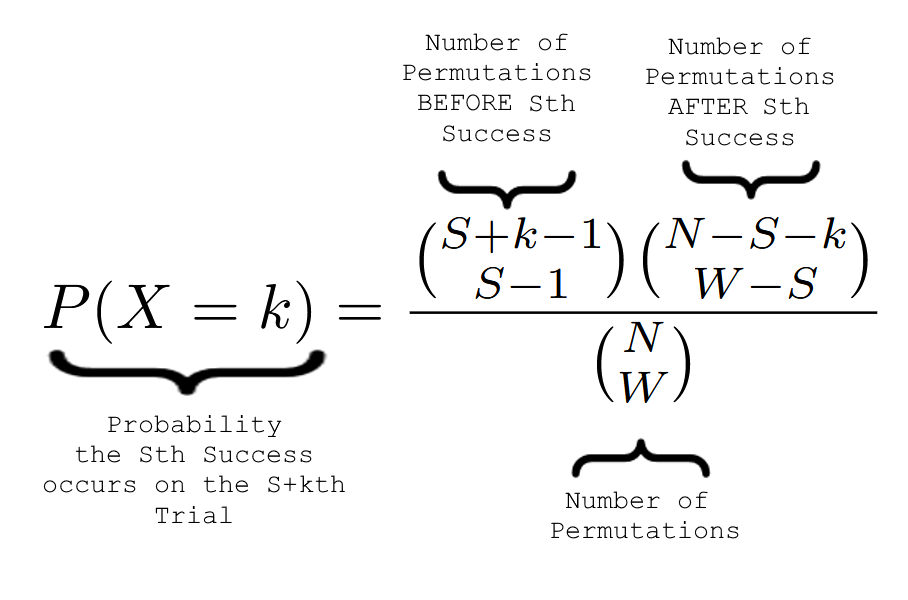
To recap, the Negative Hypergeometric distribution tells us that, if we have a ball with W white balls and N balls, of which we want S white balls, the likelihood that we get that many balls on the S + kth draw.

The Expectation of the Negative Hypergeometric Distribution

This is more of a footnote, as I have no intention of computing an unwieldy summation or doing a roundabout proof with indicator variables, but I do think the expectation of NegHyperGeo is worth a mention.

Citations

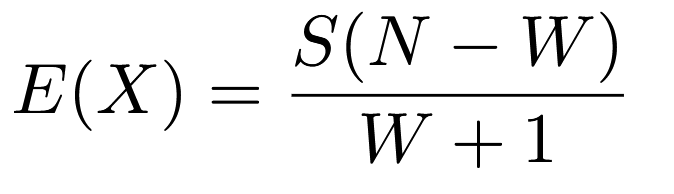
The textbook I most closely modeled my guide on was Blitzstein and Hwang's Introduction to Probability.

Contact

I've enjoyed putting together this website. Full credit to the Monospace Web, who created the template used for this.

If you'd like to contact me, my information is below

Brendan Heaney, Binghamton University Class of 2027

Personal Email: brendantheaney@gmail.com

University Email: bheaney@binghamton.edu

My LinkedIn

Homepage